在这个文章中，将模拟递归在系统中运行的过程，一来帮助大家对递归理解更深入一些，二来在关键时候，可以规避递归栈的限制。

上次文章说过，递归就是多重函数调用，函数将自己的运行状态保存起来，然后转而去调用其他函数去了，等到函数返回继续在原地执行。

假设说你要修电脑，先要用螺丝刀把机箱给打开，然后。。。
等等，螺丝刀呢？没有螺丝刀咋办，买呗，于是你就把电脑丢下，跑出去买了一个螺丝刀
买回来之后，继续把机箱打开，发现内存条坏了，于是你就把电脑丢下，跑出去买了一个内存条（这里有个细节，机箱你是打开的，有两种做法，一种是打开着的机箱丢在地上，等买完内存条再回来继续，一种是把打开着的机箱装回去，等买完内存条再回来重新拆）

我们来看一个真实的递归例子，后序优先遍历（leetcode-145）

1
2
3
4
5
6
7
8

void dfs(TreeNode* root) {
    if (root == NULL) {
        return;
    }
    dfs(root->left);
    dfs(root->right);
    visit(root); //前中后序的代码就区别于visit(root)的位置，放在两个dfs前面就是前序，放在两个dfs之间就是中序，本质上没什么区别
}

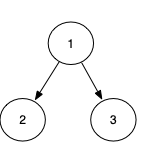
我们从代码层面上来解释上图的代码执行过程：

• 执行节点1，需要先执行左节点，挂起，节点2进入待执行栈
• 执行节点2，需要先执行左节点，挂起，节点2的左节点进入待执行栈
• 栈顶元素是个null，弹出
• 继续执行节点2，先前执行到左节点那个地方，继续，需要先执行右节点，挂起，节点2的右节点进入待执行栈
• 栈顶元素是个null，弹出
• 继续执行节点2，先前执行到右节点那个地方，继续，访问节点2，结束，弹出
• 继续执行节点1，先前执行到左节点那个地方，继续，需要先执行右节点，挂起，节点3进入待执行栈
• 执行节点3，需要先执行左节点，挂起，节点3的左节点进入待执行栈
• 栈顶元素是个null，弹出
• 执行执行节点3，先前执行到左节点那个地方，继续，需要先执行右节点，挂起，节点3的右节点进入待执行栈
• 栈顶元素是个null，弹出
• 继续执行节点3，先前执行到右节点那个地方，继续，访问节点3，结束，弹出
• 继续执行节点1，先前执行到右节点那个地方，继续，访问节点1，结束，弹出
• 栈为空，执行完毕

理解完这个递归的过程后，我们的非递归代码就呼之欲出了

• 定义一个数据类型，用来保存递归过程中的上下文，比如，各种临时变量，在递归的过程中，这些变量语言层面上帮我们解决了上下文保留，非递归版本我们需要自己保存
• 分解递归函数代码，将需要递归调用函数的部分分开，变成步骤1，步骤2，。。。例如，上面的后续优先遍历，就分成3个步骤，1是从开头到递归调用左节点之前，2是调用左节点后，调用右节点之前，3是调用右节点之后。

于是非递归版本的代码就是这样的：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32

struct Context {
    TreeNode* root;
    int step;
    Process(TreeNode* _root) {
        root = _root;
        step = 0;
    }
};

void artidfs(TreeNode* root) {
    vector<Context> stack;
    stack.push_back(Context(root));
    while (!stack.empty()) {
        int last = stack.size() - 1;
        if (stack[last].root == NULL) {
            //对标dfs函数中第一行，root为空，直接返回
            stack.pop_back();
        } else if (stack[last].step == 0) {
            //处于第一个阶段中
            stack[last].step++;
            stack.push_back(Context(stack[last].root->left));
        } else if (stack[last].step == 1) {
            //处于第二个阶段
            stack[last].step++;
            stack.push_back(Context(stack[last].root->right));
        } else {
            //处于第三个阶段
            visit(Context(stack[last].root));
            stack.pop_back();
        }
    }
}

这个代码基本上是通用的，大家可以尝试着改写其他递归代码，可以加深对递归的理解。

大家理解完这个代码后，再思考下为啥语言中有递归栈层数和递归中内存使用的限制。