记忆化搜索说白了就是做缓存。前面说到，函数尽可能写成跟环境无关，也就是，同一个状态必对应同一个返回值，那么我们就可以对任意函数状态进行缓存。

• 级别：为函数做缓存
• 条件：函数与环境无关
• 做法：以函数状态为key，以函数值为value，做映射

例子：

斐波那契数列，求第n项

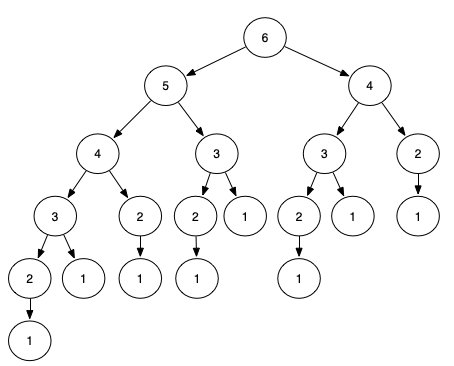
这图是求斐波那契数列第6项的搜索树。可以看出，计算第6项需要计算第4项的结果，计算第5项也需要计算第4项的结果，为了避免重复计算，我们需要将计算第4项的结果缓存起来，以便重复使用

1
2
3
4
5
6
7
8
9
10
11
12

int cache[N]; //n如果有确切的范围，并且n比较小时，我们可以开个数组来存储函数值，存取函数值只有o(1)的复杂度
// map<int, int> cache; //如果没有确切的范围，或者n比较大时，我们需要利用映射数据结构来存储函数值，比如红黑树、哈希表
memset(cache, -1, sizeof(cache)); //-1表示cache还没计算过
int f(int n) {
    if (n <= 2) {
        return 1;
    }
    if (cache[n] != -1) {
        return cache[n];    
    }
    return cache[n] = f(n - 1) + f(n - 2);
}

上面是个cpp代码，如果用python写，那就更简单了，在函数上写个注解@lru_cache(maxsize=N)即可
记忆化搜索是非常通用的，在求存在递推方程的题目中，不管是状态空间大还是小，记忆化搜索都能解决。唯一不足的是由于记忆化搜索通常用递归来实现，递归层数不能太多，否则会出现stackoverflow的异常。

习题：leetcode-202
体验一下无法递推，只能使用记忆化搜索的题目