上一篇说到,函数是将状态通过计算逻辑产生函数值。
我们用一个最经典的例子来解释一下递归:
计算第n项斐波那契数列
斐波那契数列的数学递推公式是f(n)=f(n-1)+f(n-2),我们把这个公式转成代码:
1 | int f(int n) { |
这就是递归。计算n的过程中,需要n-1和n-2的函数值,而计算n,n-1,n-2的函数值,都是相同的逻辑,所以函数f中调用了函数f
注意:不要把递归理解成自己调用自己,而要理解成,计算状态值,用到了另一个状态值
举个类似的例子:
假设说你要修电脑,先要用螺丝刀把机箱给打开,然后。。。
等等,螺丝刀呢?没有螺丝刀咋办,买呗,于是你就把电脑丢下,跑出去买了一个螺丝刀
买回来之后,继续把机箱打开,发现内存条坏了,于是你就把电脑丢下,跑出去买了一个内存条(这里有个细节,机箱你是打开的,有两种做法,一种是打开着的机箱丢在地上,等买完内存条再回来继续,一种是把打开着的机箱装回去,等买完内存条再回来重新拆)
根据这个例子,再想一下什么是递归。其实函数调用就是一个父任务,计算父任务时,需要子任务一,于是代码中把父任务挂起,先执行子任务,等到子任务执行完之后,再把结果返回到父任务这里
递归,只是因为父任务跟子任务干同样的事情而已
(刚才例子说了有两种做法,一种对应的函数嵌套调用,另一种,是不是跟callback有异曲同工之妙啊)
递归是状态之间的依赖和联系,见下图:
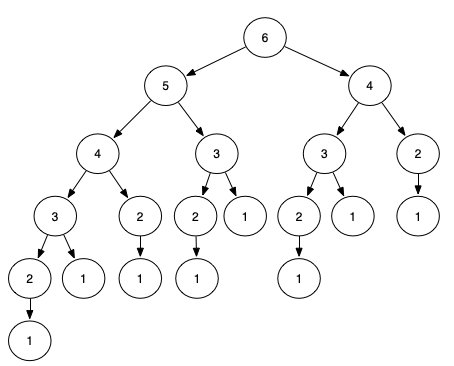
看这图,递归能否退出有两个条件:
- 没有环路
- 有叶子节点
我们在设计递归函数时,考虑下面几个要素:
- 状态空间是什么,状态由哪几个变量组成(动态规划就是通过转换状态获得状态空间的缩小)
- 状态函数值的依赖关系
- 终止条件
递归和递推
在动态规划中,往往递推是大部分人选择的方式,但是动态规划跟递推其实没有半毛钱关系,递推只是实现的方式
递推写法可以写成递归的方式,这就是常说的自顶而下还是自底而上
反过来,递归的方式也可以写成递推写法,但是有时候递推顺序并不是按数字顺序来
比如:f(n) = f(n-1)+f(n+1) (n为奇数) f(n) = f(n / 2) (n为偶数)
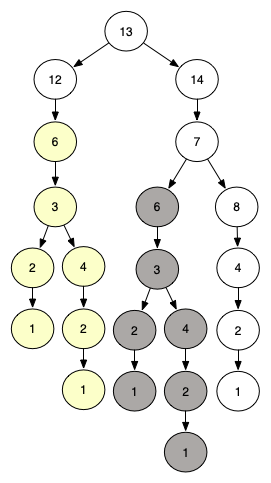
看着图,节点9,10,都是不存在的。实际上,递归写法转成递推写法是按照拓扑序来递推,只是斐波那契数列的拓扑序正好是1到n,至于拓扑序是什么,后面讲
解题建议
很多人会纠结自顶而下还是自底而上的写法,这里建议,解题就是用自顶而下的思想,没有其他的。拿到一个题目,先从要求的函数值进行倒推,求这个状态,需要先求另个状态,这样推过去。能用记忆化搜索用记忆化搜索;递归层数太多时,再想想拓扑序是什么,转换后进行递推,如果拓扑序本身需要递归推出来,那么直接记忆化搜索就行了
动态规划也一样,推出递推方程之后,不要急着动手,先想想记忆化搜索的写法,脑中有一颗递归树,再判断递归树中有多少个节点,有什么状态,状态空间多大;再判断拓扑序,写成递推的形式
