推荐读本《图算法》
拓扑排序
拓扑排序是一种应用广泛的图算法,通常见于任务DAG图的执行排序,由于任务图有依赖,必须优先执行上游任务再逐步解锁下游任务,因此执行顺序至关重要。
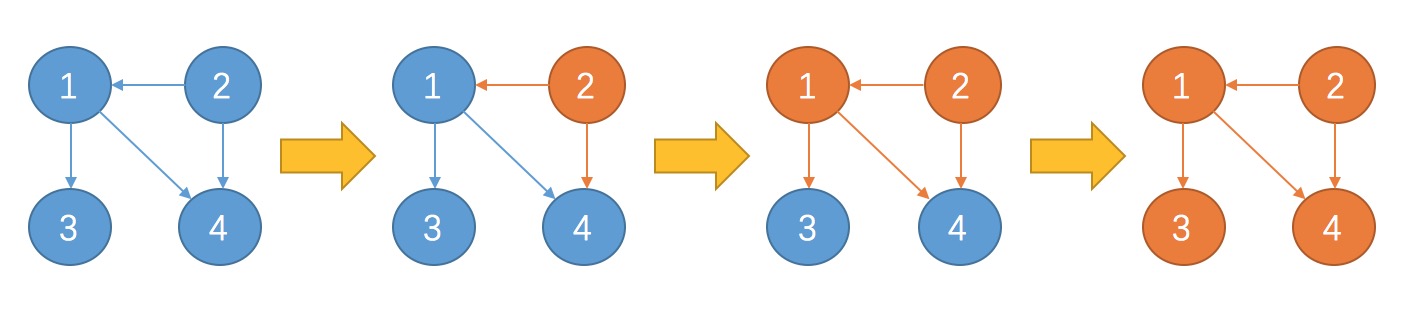
拓扑排序主要思想是:
- 访问入度为0的点(访问没有上游任务依赖的节点)
- 将下游的依赖点入度减1(下游任务检测到一个依赖任务已经完成)
- 循环前面两个步骤,直到所有点都被访问
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
| public static class Node {
List<Node> children;
}
public static List<Node> topsort(List<Node> nodes) {
List<Node> result = new ArrayList<Node>();//已经排好序的列表
Map<Node, Integer> num_parent = new HashMap<Node, Integer>();//上游点的个数
for (Node node : nodes) {
if (!num_parent.containsKey(node)) {
num_parent.put(node, 0);
}
for (Node child : node.children) {
//对每个下游,累加,如果node数据结构有指向上游节点的引用,就不用这么计算
num_parent.compute(child, new BiFunction<Node, Integer, Integer>() {
public Integer apply(Node node, Integer number) {
if (number == null) {
return 1;
} else {
return number + 1;
}
}
});
}
}
Queue<Node> ready = new ArrayDeque<Node>();
for (Node node : nodes) {
//第一轮没有上游节点的节点,可以优先计算
if (num_parent.get(node) == 0) {
ready.add(node);
}
}
while (!ready.isEmpty()) {
//execute(ready); 这里可以多个节点一起取,这些节点是没有互相之间的依赖,可以以任意顺序访问
Node current = ready.poll();
result.add(current);
for (Node child : current.children) {
num_parent.compute(child, new BiFunction<Node, Integer, Integer>() {
public Integer apply(Node node, Integer number) {
return number - 1;
}
});
if (num_parent.get(child) == 0) {
ready.add(child);
}
}
}
return result;
}
|

